Date: Thu, 22 Jan 2015 23:56:14 +0100
Hi,
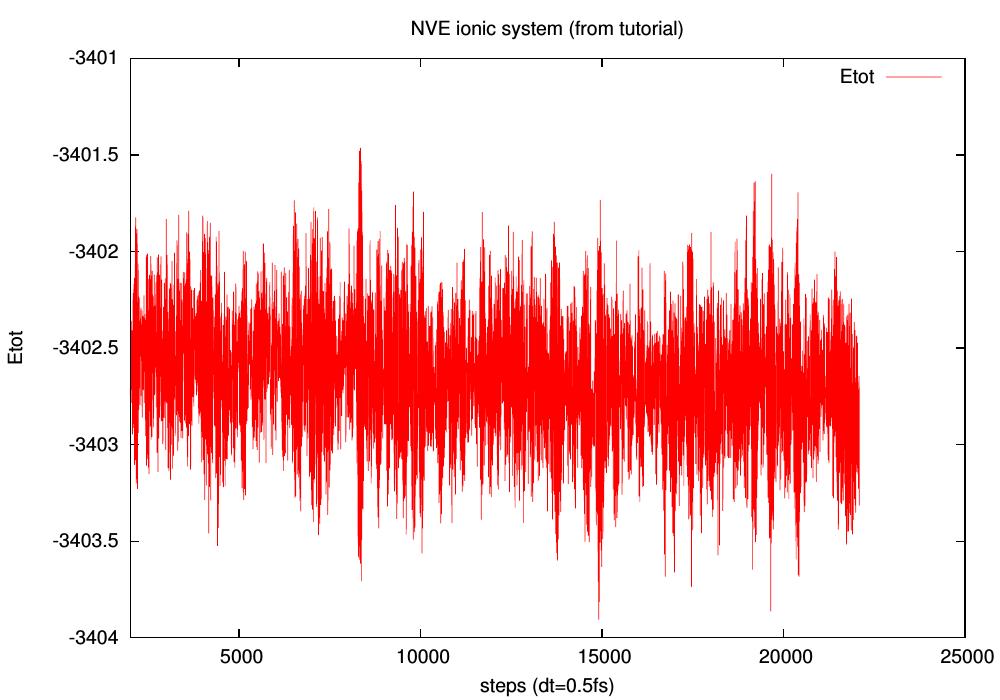
I'm making some tests after building the ionic system as explained in
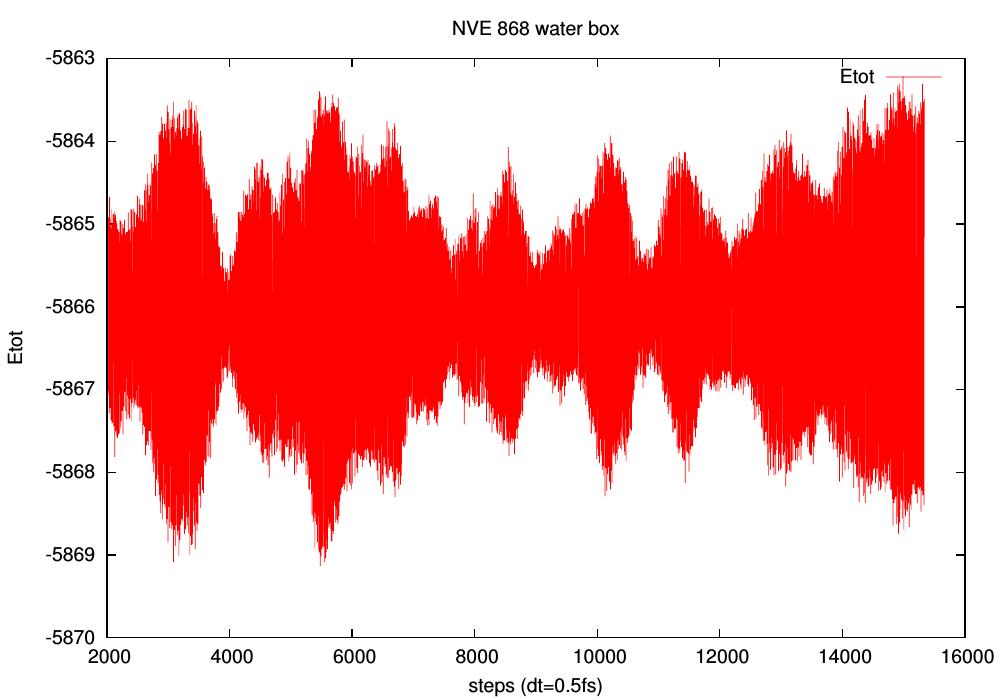
the tutorial and comparing with box of waters (4096, 1728, and 868 H2O).
NVE seems OK for water, less for the ionic system (see pictures).
However, energy fluctuations seem larger for water (~2500 atoms,
compared to ~4000 for the ionic one). How do you compute your energy drift?
Btw, I'm using dt=0.5fs, no shake + ewald (no difference between Ewald
and PME for this):
&ewald
skinnb = 3.0,
dsum_tol = 1e-9,
nfft1 = 128,
nfft2 = 128,
nfft3 = 128,
ew_type = 1,
rsum_tol = 1e-9,
eedmeth = 3,
/
Gerald.
On 01/22/2015 11:22 PM, Joseph Baker wrote:
> Hi Jason,
>
> Thanks for the reply. I will try playing with the SHAKE tolerance to see
> what happens with dt=0.002. I guess I should also point out that we we were
> also seeing worse-than-typical energy conservation for the cases where we
> were using dt=0.001 and no SHAKE at all, so that wouldn't explain those
> cases I guess?
>
> I tried adjusting rsum_tol just now and was given the error that rsum_tol
> is only used if ew_type = 1, so I tried setting ew_type to 1 (default is
> 0), and then get the error that ew_type must be 0 for pmemd. So apparently
> this is not changeable when using pmemd? I'll try adjusting just dsum_tol
> down a few orders of magnitude and see how that influences the drift.
>
> I appreciate the suggestions.
>
> Joe
>
>
> On Thu, Jan 22, 2015 at 4:28 PM, Jason Swails <jason.swails.gmail.com>
> wrote:
>
>> On Thu, Jan 22, 2015 at 3:37 PM, Joseph Baker <bakerj.tcnj.edu> wrote:
>>
>>> Gerald, the molecules are the ones in the amber ionic liquid tutorial, so
>>> bigger than water. I just tried to set skinnb = 4.0 under &ewald in my
>>> input script, and am getting basically the same behavior as with the
>>> default skinnb (total energy vs time stays roughly flat for ~ 1 ns or so,
>>> and then starts to really shoot up, giving an overall drift of about 6 x
>>> 10^-4 kT/ns/dof).
>>>
>>
>> I'm not sure if this was always true, but in the current versions of the
>> code skinnb has no effect at all on the results (just in efficiency). [1]
>>
>> Jason, I was not using SHAKE in the 1 fs timestep runs, however in the 2 fs
>>> runs I did. I have two runs (that started from different annealing
>>> protocols, so this is not really comparing apples to apples I suppose)
>> and
>>> those used the following parameters
>>>
>>> dt = 0.002
>>> ntc=ntf=2
>>> And default values for tol and dsum_tol
>>> Results in drift = 1.0 x 10^-2 kT/ns/dof
>>>
>>> dt = 0.002
>>> ntc=ntf=2
>>> tol = 0.000001
>>> dsum_tol = 0.000001
>>> Results in drift = 2.6 x 10^-3 kT/ns/dof
>>>
>>
>> I suspect this is largely due to the tolerance changes. You could always
>> compute the forces for each starting position and compare them, but I
>> suspect the distribution of force magnitudes will be roughly the same
>> (which I think is really what matters most to an integrator wrt time-step
>> dependence of energy drift).
>>
>> This makes it appear that there is almost an order of magnitude improvement
>>> in the drift when those tolerance values are changed, however, the second
>>> case was the result of a longer (and probably better) annealing scheme.
>> If
>>> you don't think that this is telling, I can run a more controlled test of
>>> the tolerance parameter by using the same starting configuration in each
>>> case. Is it worth is to make the tolerance even smaller than 10^-6?
>>
>>
>> I don't run much NVE myself, but I *think* I recall seeing that my
>> colleagues that _do_ set tol=1e-8. The default SHAKE tolerance is 1e-5, so
>> you've only reduced it by 1 order of magnitude. At some point that will
>> stop being a significant contribution to the integration error, but I don't
>> know for sure what point that is.
>>
>> To be honest, I'm not sure what dsum_tol and rsum_tol *really* do, but
>> based on a brief code inspection here it is: I think dsum_tol is used to
>> determine the width of neutralizing charge distributions (i.e., the Ewald
>> coefficient). It is chosen so that the error in erfc at the cutoff falls
>> below the tolerance.
>>
>> This Ewald coefficient, though, has a direct impact on the error in the
>> reciprocal space sum, too. The narrower you make the Gaussian charge
>> distributions, the faster the direct space sum decays, but the more
>> frequencies you need in the reciprocal lattice vectors to fit to the (more
>> jagged) charge distribution. So even though you made dsum_tol small, the
>> error in the reciprocal space sum could still be the primary contributor to
>> your energy drift.
>>
>> I would suggest *also* decreasing rsum_tol by an order of magnitude (or
>> more) and see if that helps clean up the drift for you. I *think* that
>> making both dsum_tol and rsum_tol small will force pmemd to use a small
>> Ewald coefficient with a large number of reciprocal vectors (enough recip.
>> vectors to force the reciprocal sum error to fall below rsum_tol). If
>> that's true, then this should help. If it's not, then I'm outta ideas :).
>>
>>
>> Good luck,
>> Jason
>>
>> --
>> Jason M. Swails
>> BioMaPS,
>> Rutgers University
>> Postdoctoral Researcher
>> _______________________________________________
>> AMBER mailing list
>> AMBER.ambermd.org
>> http://lists.ambermd.org/mailman/listinfo/amber
>>
> _______________________________________________
> AMBER mailing list
> AMBER.ambermd.org
> http://lists.ambermd.org/mailman/listinfo/amber
>
-- ____________________________________________________________________________ Prof. Gerald MONARD SRSMC, Université de Lorraine, CNRS Boulevard des Aiguillettes B.P. 70239 F-54506 Vandoeuvre-les-Nancy, FRANCE e-mail : Gerald.Monard.univ-lorraine.fr tel. : +33 (0)383.684.381 fax : +33 (0)383.684.371 web : http://www.monard.info ____________________________________________________________________________
_______________________________________________
AMBER mailing list
AMBER.ambermd.org
http://lists.ambermd.org/mailman/listinfo/amber
(image/jpeg attachment: water-1.jpg)
(image/jpeg attachment: ionic-1.jpg)
