Date: Mon, 9 Dec 2024 21:59:18 +0000
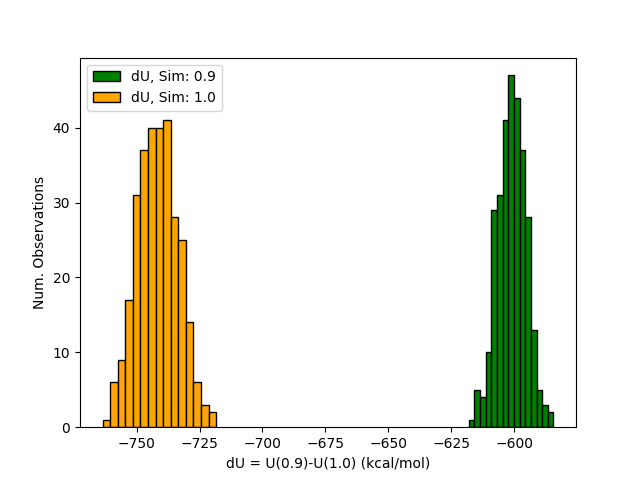
I took a look at your lambda=0.9 and lambda=1.0 simulations to try and figure out what might be going on. Each simulation contains "MBAR Energy analysis" sections in the mdout files. Let us define dU = U(r;lambda=1.0)-U(r;lambda=0.9). One can calculate the dU timeseries using the data from the lambda=0.9 simulation, and one can similarly calculate another dU timeseries using the data from the lambda=1.0 simulation. The two dU timeseries can be histogrammed to compare their distributions. I have attached an image of the distributions to this email. Unlike the TI method, the FEP, BAR, MBAR methods require overlap between these distributions to obtain a reasonable result. Your distributions are separated by a large 100 kcal/mol gap, however. Normally, edgembar will solve the MBAR equations and tell you if the results are unreliable due to poor phase space overlap. I believe the problem is that your phase space overlap is so bad that it is actually causing numerical issues that prevent the nonlinear optimizer from working properly. I'll have to think about how the program should identify these situations and offer the user guidance.
My interpretation is that you are using a 3-stage protocol (decharge, van der waals, recharge) with the traditional lambda scheduling. Furthermore, the dU/dL profile in the vdW stage (in the python script you originally attached) appears to exhibit weird end-point behavior near lambda=1. Perhaps it might be worthwhile to instead try the 1-stage smoothstep softcore potential. This approach makes a simultaneous change to the vdW and electrostatic interactions, but the lambda-dependence leads to more stable TI profiles which will likely also improve the phase space overlap. To try this, the mdin file would be very similar to your vdW inputs, however, leave crgmask blank (do not zero out any charges), and set gti_lam_sch=1
I'm looking at an example that someone else ran, and their options look like this:
clambda = 1.00000000 ! current lambda window
timask1 = '.1-21' ! TI region 1
timask2 = '.22-42' ! TI region 2
crgmask = ""
scmask1 = '.6-8,17-19' ! softcore region 1
scmask2 = '.27-28,37-40' ! softcore region 2
scalpha = 0.5 ! = 0.5 when gti_scale_beta = 1
scbeta = 1.0 ! = 1.0 when gti_scale_beta = 1
gti_cut = 1 ! internal softcore non-bonded terms will not be cu
gti_output = 1 ! = 1, output detailed TI results
gti_add_sc = 25 ! = 25, energy terms to be scaled by lambda
gti_scale_beta = 1 ! = 1, use the softcore potential form 25.13 in Ambe
gti_cut_sc_on = 6 ! distance to smooth softcore potential begin at (This is the value of "cut" - 2 Ang)
gti_cut_sc_off = 8 ! distance to smooth softcore potential stop at (This is the value of "cut")
gti_lam_sch = 1 ! = 1, lambda replaced by smoothstep lambda
gti_ele_sc = 1 ! = 1, softcore smoothstep electrostatic potential
gti_vdw_sc = 1 ! = 1, softcore smoothstep vdW potential
gti_cut_sc = 2 ! = 2, smooth both electrostatic and vdW
gti_ele_exp = 2 ! = 2, best practice
gti_vdw_exp = 2 ! = 2, best practice
gremd_acyc = 1 ! = 1, not exchange lambda = 0 with lambda
Note that I set the gti_cut_sc_on and gti_cut_sc_off values to 6 and 8 because you had set the cutoff to cut=8. These values would instead be 8 and 10 if your cutoff was cut=10, for example.
Although I wrote the analysis program, I don't actually perform alchemical free energy simulations. If an expert is reading this who runs these simulations, please feel free to offer guidance or make corrections.
_______________________________________________
AMBER mailing list
AMBER.ambermd.org
http://lists.ambermd.org/mailman/listinfo/amber
(image/png attachment: Distributions.png)
