Date: Wed, 15 Nov 2017 00:32:33 +0300
Hello community!
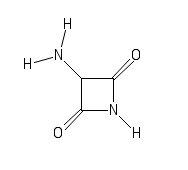
We are working on parameterizing of some molecule (6-aminopenicillanic
acid) and for these moment we are trying to find right dihedral terms for
hydrogens attached to nitrogen (we're rotating NH2 group). Because of
tricky nature of the 6-APA we're decided to 'decompose' molecule to set of
smaller fragments. One of these molecules: C1(C(=O)N(C1=O)[H])N([H])[H]
(SMILES)
After geomeptry optimization in Gaussian and RESP charge fitting we rotated
the NH2 group around N-C bond with stepping of 5.0 degrees (full circle)
and conducted single-point energies run at Gaussian (according to the
"paramfit" manual at ambermd.org). So we have potential energy profile for
NH2 rotating.
As we understand it these energy profile contains not only dihedral
interactions of hydrogens on amino group but also van der Waals and
electrostatics with other atoms in molecule. We assigned basic parameters
from GAFF field with parmchk2 and decided to fit energy term for H-N-C-C
dihedral but not with plain paramfit.
As soon as we know the Amber energy is: E = bonds + angles + dihedrals +
vdw + el
So for the first step we set Kp value for H-N-C-C dihedral term to 0 (in
hope that in result we obtain all energy terms with these one excepted: E =
bonds + angles + dihedrals* + vdw + el). For the sake of simplicity we're
conducted dummy fit of the K value with paramfit and get MM energies from
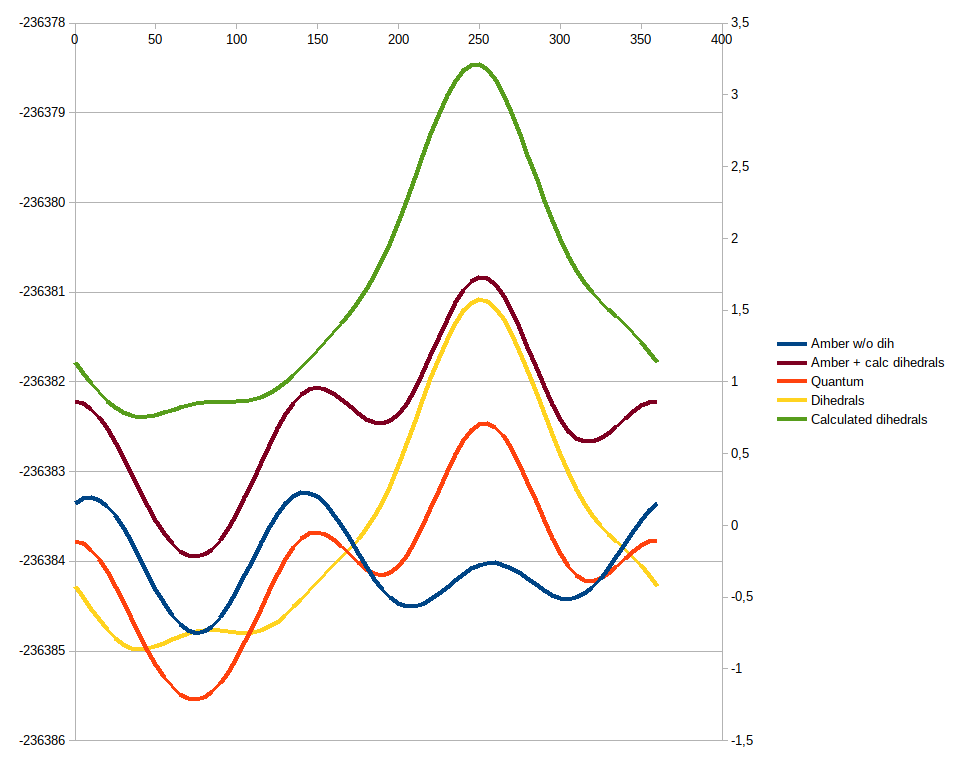
the output file (WRITE_ENERGY is set in job control file). After that we
subtracted these energies (blue line) from quantum data (orange line) in
hope that now we will have pure dihedral energy dependency on the angle of
NH2 rotation (yellow line). All these dependencies are on attached plot
[image: Встроенное изображение 2]
As soon as we obtained pure dihedral energy profile we conducted the FFT
transform on these data and obtained Fourier coefficients and phase shifts.
We are decided to get the first 4 harmonics of Fourier series (because of
high amplitude density) and discarded null coefficient because it's only
matter of fitting the K value soon:
Np Kp Phase
1 1.06514231 -111.231865
2 0.32663696 137.269480
3 0.13145744 7.266503
4 0.08701518 -77.208482
Then we constructed energy profile back with this formula:
E(phi) = Kp_1 * (1 + cos(phi + phase_1)) + Kp_2 * (1 + cos(2 * phi +
phase_2)) + Kp_3 * (1 + cos(3 * phi + phase_3) + Kp_4 * (1 + cos(4 * phi +
phase_4))
The result is shown on the image above (green line; compare with the yellow
line - only vertical shift is needed...). Seems like the results obtained
are in good agreement with our assumptions (brown line; compare with the
orange one). For the frcmod file we're inverting signs of phases (as soon
as Amber requires E(phi) = Vn * (1 + cos(n * phi - gamma_n)))
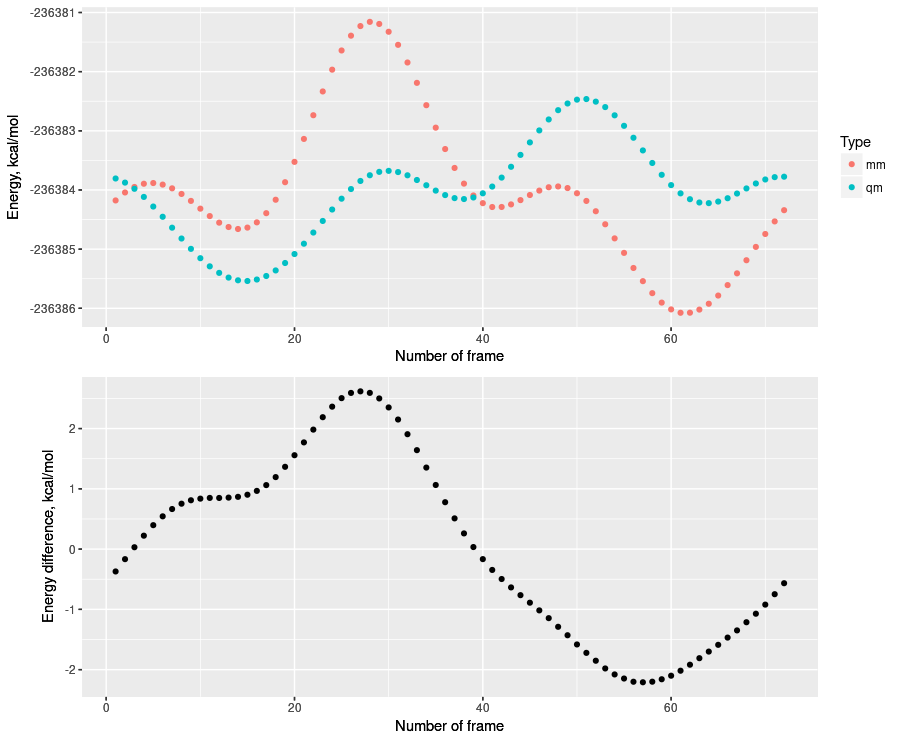
After that we edited frcmod again and now replaced old term for H-N-C-C
dihedral with four new with parameters from FFT analysis. But next things
went bad. After fitting the K value we can't get right energy profile as
brown line on above plot! Things are messed up[image: Встроенное
изображение 3]
We are supposing that paramfit needs some transformed angles on its input
or we are need to apply shift to our phases (already tried pi, -pi and sign
inversion). Other thoughts that some mess are on the stage of getting pure
dihedral energies...
Can you help us? We're completely stuck upon it. Blind fit of phases and/or
Kp's in paramfit gives us physically non-sense values so we want to do that
on concrete basis. Thank you!
-- С уважением, Дробот Виктор
_______________________________________________
AMBER mailing list
AMBER.ambermd.org
http://lists.ambermd.org/mailman/listinfo/amber
(image/png attachment: ______________________.png)
(image/png attachment: 02-______________________.png)
(image/png attachment: __________________________2017-11-15_00-00-37.png)
